微分法の方程式への応用 (文系・理系共通)
微分法の方程式への応用
問題《チェビシェフ多項式にまつわる方程式》
$a$ を実数の定数とする.
- (A)
- $4x^3-3x = a$
- (B)
- $8x^4-8x^2+1 = a$
解答例
- (A)
- $f(x) = 4x^3-3x$ とおく.
このとき,
\[\begin{aligned}
f'(x) &= 12x^2-3 = 12\left( x^2-\frac{1}{4}\right) \\
&= 12\left( x+\frac{1}{2}\right)\left( x-\frac{1}{2}\right)
\end{aligned}\]
から, $f(x)$ の増減は下の表のようになる.
よって, $f(x)$ は, $x = -\dfrac{1}{2}$ のとき極大値 $1,$ $x = \dfrac{1}{2}$ のとき極小値 $-1$ をとり, $f(x)$ のグラフ $y = f(x)$ の概形は下の図のようになる.
$x$ $\cdots$ $-\dfrac{1}{2}$ $\cdots$ $\dfrac{1}{2}$ $\cdots$ $f'(x)$ $+$ $0$ $-$ $0$ $+$ $f(x)$ $\nearrow$ 極大 $\searrow$ 極小 $\nearrow$ ゆえに, 与えられた方程式 $f(x) = a$ の異なる実数解の個数は, 曲線 $y = f(x)$ と直線 $y = a$ の共有点の個数に等しく, $a < -1,$ $1 < a$ のとき $1$ 個, $a = \pm 1$ のとき $2$ 個, $-1 < a < 1$ のとき $3$ 個である.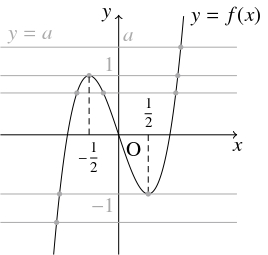
- (B)
- $g(x) = 8x^4-8x^2+1$ とおく.
このとき,
\[\begin{aligned}
g'(x) &= 32x^3-16x = 32x\left( x^2-\dfrac{1}{2}\right) \\
&= 32x\left( x+\frac{1}{\sqrt 2}\right)\left( x-\frac{1}{\sqrt 2}\right)
\end{aligned}\]
から, $g(x)$ の増減は下の表のようになる.
よって, $g(x)$ は, $x = 0$ のとき極大値 $1,$ $x = \pm\dfrac{1}{\sqrt 2}$ のとき極小値 $-1$ をとり, $g(x)$ のグラフ $y = g(x)$ の概形は下の図のようになる.
$x$ $\cdots$ $-\dfrac{1}{\sqrt 2}$ $\cdots$ $0$ $\cdots$ $\dfrac{1}{\sqrt 2}$ $\cdots$ $g'(x)$ $-$ $0$ $+$ $0$ $-$ $0$ $+$ $g(x)$ $\searrow$ 極小 $\nearrow$ 極大 $\searrow$ 極小 $\nearrow$ ゆえに, 与えられた方程式 $g(x) = a$ の異なる実数解の個数は, 曲線 $y = g(x)$ と直線 $y = a$ の共有点の個数に等しく, $a < -1$ のとき $0$ 個, $a = -1,$ $a > 1$ のとき $2$ 個, $a = 1$ のとき $3$ 個, $-1 < a < 1$ のとき $4$ 個である.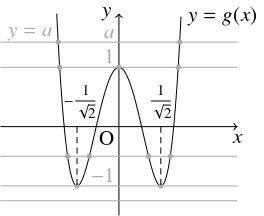
参考
$3$ 倍角, $4$ 倍角の公式から, 上記の関数 $f(x) = 4x^3-3x,$ $g(x) = 8x^4-8x^2+1$ は $\cos 3\theta = f(\cos\theta ),$ $\cos 4\theta = g(\cos\theta )$ を満たす.
このように, $\cos n\theta = T_n(\cos\theta )$ を満たす多項式 $T_n(x)$ を「第一種チェビシェフ多項式」(Chebyshev polynomial of the first kind) と呼ぶ (こちらを参照).
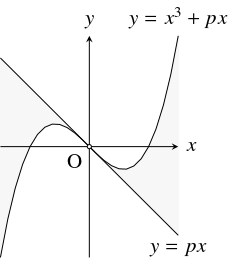
問題《$3$ 次関数のグラフの接線の交点の分布》
曲線 $C:y = x^3+px$ $(p \neq 0)$ の複数本の接線の交点の存在範囲を求めよ.
解答例
$y = x^3+px$ の導関数は
\[ y' = 3x^2+p\]
であるから, 点 $(s,s^3+ps)$ における $C$ の接線の方程式は
\[\begin{aligned}
y-(s^3+ps) &= (3s^2+p)(x-s) \\
y &= (3s^2+p)x-2s^3
\end{aligned}\]
である.
この直線が点 $\mathrm P(a,b)$ を通るとき,
\[ b = -2s^3+3as^2+ap\]
が成り立つ.
そこで, $a,$ $b$ を実数として, 関数 $f(s) = -2s^3+3as^2+ap$ のグラフ $t = f(s)$ と直線 $t = b$ が複数の共有点をもつような条件を調べる.
$f(s)$ を微分すると,
\[ f'(s) = -6s^2+6as = -6s(s-a)\]
となる.
- (i)
- $a > 0$ のとき.
$f(s)$ の増減は次の表の通りであるから, $t = f(s)$ と $t = b$ が複数の共有点をもつ条件は $ap \leqq b \leqq a^3+ap$ である.
共有点の個数は, $b = ap,$ $a^3+ap$ のとき $2$ 個, $ap < b < a^3+ap$ のとき $3$ 個である.
$s$ $\cdots$ $0$ $\cdots$ $a$ $\cdots$ $f'(s)$ $-$ $0$ $+$ $0$ $-$ $f(s)$ $\searrow$ $ap$ $\nearrow$ $a^3+ap$ $\searrow$ 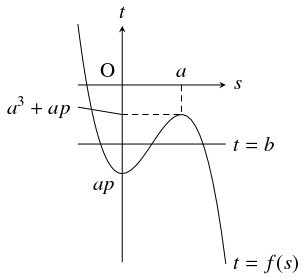
- (ii)
- $a = 0$ のとき. $f(s)$ は単調減少になり, 極値をもたないから, $t = f(s)$ と $t = b$ が複数の共有点をもつことはない.
- (iii)
- $a < 0$ のとき.
$f(s)$ の増減は次の表の通りであるから, $t = f(s)$ と $t = b$ が複数の共有点をもつ条件は $a^3+ap \leqq b \leqq ap$ である.
共有点の個数は, $b = a^3+ap,$ $ap$ のとき $2$ 個, $a^3+ap < b < ap$ のとき $3$ 個である.
$s$ $\cdots$ $a$ $\cdots$ $0$ $\cdots$ $f'(s)$ $-$ $0$ $+$ $0$ $-$ $f(s)$ $\searrow$ $a^3+ap$ $\nearrow$ $ap$ $\searrow$ 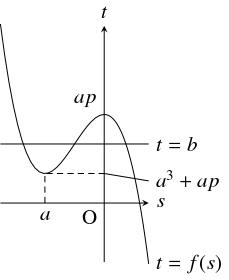

解説
平行移動, 対称移動と $y$ 座標の定数倍を考えると, 次のことがわかる:
極値をもつ $3$ 次関数のグラフ $C$ が点 $\mathrm S$ に関して対称で, $C$ の $\mathrm S$ における接線が $l$ であるとき,
$C$ の $2$ 本の接線の交点の存在範囲は $C$ の $\mathrm S$ を除く部分であり,
$C$ の $3$ 本の接線の交点の存在範囲は $C$ と $l$ に挟まれた部分である.
