接線 (文系・理系共通)
接線
定理《関数のグラフの接線》
$x = t$ において微分可能な関数 $f(x)$ のグラフ $y = f(x)$ の点 $(t,f(t))$ における接線の方程式は
\[ y = f'(t)(x-t)+f(t)\]
である.
定理《関数のグラフの共通接線》
$x = t$ において微分可能な関数 $f(x),$ $g(x)$ に対して,
が成り立つ.
| 曲線 $y = f(x),$ $y = g(x)$ が直線 $x = t$ 上で共通接線をもつ |
| $\iff$ $f(t) = g(t),$ $f'(t) = g'(t)$ |
証明
曲線 $y = f(x),$ $y = g(x)$ の点 $(t,f(t)),$ $(t,g(t))$ における接線の方程式はそれぞれ
\[ y = f'(t)(x-t)+f(t), \quad y = g'(t)(x-t)+g(t)\]
であるから,
が成り立つ.
| 曲線 $y = f(x),$ $y = g(x)$ が直線 $x = t$ 上で共通接線をもつ |
| $\iff$ $f'(t)(x-t)+f(t) = g'(t)(x-t)+g(t)$ |
| $\iff$ $xf'(t)+f(t)-tf'(t) = xg'(t)+g(t)-tg'(t)$ |
| $\iff$ $f'(t) = g'(t),$ $f(t)-tf'(t) = g(t)-tg'(t)$ |
| $\iff$ $f(t) = g(t),$ $f'(t) = g'(t)$ |
問題《多項式関数のグラフと直線が接する条件》
$\alpha$ を実数, $f(x),$ $f_1(x),$ $f_2(x)$ を次数が $2$ 以上の実数係数多項式とする.
- (1)
- $f(x)$ を $(x-\alpha)^2$ で割った商を $p(x)$ とおき, その余りを $x-\alpha$ で割った商を $q,$ 余りを $r$ とおく. また, $y = f(x)$ のグラフの点 $(\alpha,f(\alpha ))$ における接線を $y = g(x)$ とする. このとき, $r = f(\alpha ),$ $q = f'(\alpha )$ であることを示すことにより, $f(x)-g(x)$ は $(x-\alpha )^2$ で割り切れることを示せ.
- (2)
- $y = f_1(x),$ $y = f_2(x)$ のグラフが直線 $x = \alpha$ 上で共有点をもち, その点における接線が一致するとする. このとき, $f_1(x)-f_2(x)$ は $(x-\alpha )^2$ で割り切れることを示せ.
解答例
- (1)
- 剰余の定理により, $r = f(\alpha )$ が成り立つ. よって, \[ f(x)-f(\alpha ) = p(x)(x-\alpha )^2+q\cdot (x-\alpha )\] であるから, 微分係数の定義により \[\begin{aligned} f'(\alpha ) &= \lim\limits_{x \to \alpha}\frac{f(x)-f(\alpha )}{x-\alpha} \\ &= \lim\limits_{x \to \alpha}\{ p(x)(x-\alpha )+q\} = q \end{aligned}\] が得られる. よって, \[ f(x) = p(x)(x-\alpha )^2+f'(\alpha )(x-\alpha )+f(\alpha )\] であり, 接線の公式により \[ g(x) = f'(\alpha )(x-\alpha )+f(\alpha )\] であるから, 辺々を引くと \[ f(x)-g(x) = p(x)(x-\alpha )^2\] となる. ゆえに, $f(x)-g(x)$ は $(x-\alpha )^2$ で割り切れる.
- (2)
- $x = \alpha$ における $y = f_1(x),$ $y = f_2(x)$ のグラフの共通の接線を $y = g(x)$ とする. (1) の結果により, $f_1(x)-g(x),$ $f_2(x)-g(x)$ は $(x-\alpha )^2$ で割り切れるから, \[ f_1(x)-f_2(x) = \{ f_1(x)-g(x)\} -\{ f_2(x)-g(x)\}\] は $(x-\alpha )^2$ で割り切れる.
参考
- 多項式 $f(x)$ が $(x-\alpha )^2$ で割り切れることと, $f(\alpha ) = f'(\alpha ) = 0$ が成り立つことは同値である (こちらを参照).
- $2$ 曲線 $C_1,$ $C_2$ が点 $\mathrm P$ を共有し, $C_1,$ $C_2$ の点 $\mathrm P$ における接線が一致するとき, $C_1,$ $C_2$ は点 $\mathrm P$ で「接する」という.
問題《放物線の接線の交点と相加・相乗平均の不等式》
放物線 $C:y = x^2$ の点 $\mathrm A(\alpha,\alpha ^2),$ $\mathrm B(\beta,\beta ^2)$ $(\alpha \neq \beta )$ における接線をそれぞれ $l_{\mathrm A},$ $l_{\mathrm B}$ とする.
- (1)
- $l_{\mathrm A}$ の方程式を求め, $l_{\mathrm A}$ の点 $\mathrm A$ を除く部分は $C$ の下方にあることを示せ.
- (2)
- $l_{\mathrm A},$ $l_{\mathrm B}$ の交点 $\mathrm M$ の座標を求めよ.
- (3)
- $\dfrac{\alpha +\beta}{2} > \sqrt{\alpha\beta}$ が成り立つことを示せ.
解答例
- (1)
- $y = x^2$ の導関数は
\[ y' = 2x\]
であるから, $C:y = x^2$ の点 $\mathrm A(\alpha,\alpha ^2)$ における接線 $l_{\mathrm A}$ の方程式は
である. \[ x^2-(2\alpha x-\alpha ^2) = (x-\alpha )^2 \geqq 0\] が成り立ち, 等号が成り立つのは $x = \alpha$ のときに限るから, $l_{\mathrm A}$ の点 $\mathrm A$ を除く部分は $C$ の下方にある.$y = 2\alpha (x-\alpha )+\alpha ^2$ つまり $y = 2\alpha x-\alpha ^2$ - (2)
- (1) と同様に, $l_{\mathrm B}$ の方程式は \[ y = 2\beta x-\beta ^2\] である. $l_{\mathrm A},$ $l_{\mathrm B}$ の交点 $\mathrm M$ の $x$ 座標は \[\begin{aligned} 2\alpha x-\alpha ^2 &= 2\beta x-\beta ^2 \\ 2(\alpha -\beta )x &= \alpha ^2-\beta ^2 \end{aligned}\] の解 \[ x = \frac{\alpha ^2-\beta ^2}{2(\alpha -\beta )} = \frac{\alpha +\beta}{2}\] であり, $y$ 座標は \[ y = 2\alpha\cdot\frac{\alpha +\beta}{2}-\alpha ^2 = \alpha\beta\] である. よって, 点 $\mathrm M$ の座標は \[\left(\frac{\alpha +\beta }{2},\alpha\beta\right)\] である.
- (3)
- (1) により $\mathrm M$ は $C$ の下方にあるから,
が成り立つ.$\left(\dfrac{\alpha +\beta }{2}\right) ^2 > \alpha\beta$ つまり $\dfrac{\alpha +\beta }{2} > \sqrt{\alpha\beta}$
問題《放物線の準線》
放物線 $y = x^2$ に向かって互いに直交する $2$ 本の接線が引けるような点 $\mathrm P$ の軌跡を求めよ.
解答例
点 $\mathrm P(X,Y)$ から放物線 $y = x^2$ に向かって互いに直交する $2$ 本の接線が引けるとして,
それらの接点を $(\alpha,\alpha ^2),$ $(\beta,\beta ^2)$ $(\alpha \neq \beta )$ とおく.
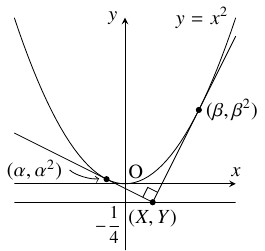 $y = x^2$ を微分すると $y' = 2x$ となるから,
点 $(\alpha,\alpha ^2)$ における接線の方程式は
$y = x^2$ を微分すると $y' = 2x$ となるから,
点 $(\alpha,\alpha ^2)$ における接線の方程式は
である.
同様に, 点 $(\beta,\beta ^2)$ における接線の方程式は
\[ y = 2\beta x-\beta ^2 \quad \cdots [2]\]
である.
$(x,y) = (X,Y)$ は連立方程式 $[1],$ $[2]$ の解であるから,
\[ X = \frac{\alpha +\beta}{2}, \quad Y = \alpha\beta\]
である.
また, $[1],$ $[2]$ は直交するので, $2\alpha\cdot 2\beta = -1$ から
\[ X = \frac{\alpha +\beta}{2}, \quad Y = -\frac{1}{4} \quad \cdots [3]\]
が成り立つ.
ここで, $\alpha,$ $\beta$ は $t$ の $2$ 次方程式
\[ t^2-(\alpha +\beta )t+\alpha\beta = 0\]
の相異なる $2$ つの実数解であるが, その判別式は
\[ (\alpha +\beta )^2-4\alpha\beta = (\alpha +\beta )^2+1 > 0\]
と正であるから, $[3]$ はすべての実数 $X$ に対して成り立つ.
ゆえに, 点 $\mathrm P$ の軌跡は, 直線 $y = -\dfrac{1}{4}$ である.

| $y-\alpha ^2 = 2\alpha (x-\alpha )$ つまり $y = 2\alpha x-\alpha ^2 \quad \cdots [1]$ |
参考
- 一般に, 放物線 $y^2 = 4px$ $(p \neq 0)$ に向かって互いに直交する $2$ 本の接線が引けるような点の軌跡は, 準線 $x = -p$ である (準線については「式と曲線」で学ぶ).
- 楕円, 双曲線に向かって互いに直交する $2$ 本の接線が引けるような点の軌跡は円周 (の一部) である.
問題《放物線の極線》
- (1)
- 放物線 $C:y = x^2$ に $2$ 本の接線が引ける点の存在範囲を求めよ.
- (2)
- (1) の範囲にある相異なる点 $\mathrm P(a,b),$ $\mathrm P'(a',b'),$ $\mathrm P''(a'',b'')$ から $C$ に引いた $2$ 本の接線の接点をそれぞれ $\mathrm T_1$ および $\mathrm T_2,$ $\mathrm T'_1$ および $\mathrm T'_2,$ $\mathrm T''_1$ および $\mathrm T''_2$ とおく.
- ①
- 直線 $\mathrm T_1\mathrm T_2$ の方程式を求めよ.
- ②
- 直線 $\mathrm T_1\mathrm T_2$ が点 $\mathrm P'$ を通るとする. このとき, 直線 $\mathrm T'_1\mathrm T'_2$ は点 $\mathrm P$ を通ることを示せ.
- ③
- 直線 $\mathrm T_1\mathrm T_2,$ $\mathrm T'_1\mathrm T'_2$ が点 $\mathrm P''$ を通るとする. このとき, 直線 $\mathrm T''_1\mathrm T''_2$ は直線 $\mathrm P\mathrm P'$ と一致することを示せ.
解答例
- (1)
- $y = x^2$ の導関数は
\[ y' = 2x\]
であるから, $C$ の点 $(s,s^2)$ における接線の方程式は
である. この直線が点 $\mathrm P(a,b)$ を通るとき, \[ b = 2as-s^2\] が成り立つ. そこで, $a,$ $b$ を定数として, 関数 $f(s) = 2as-s^2$ のグラフ $t = f(s)$ と直線 $t = b$ が $2$ 個の共有点をもつような条件を調べる. \[ f(s) = -(s-a)^2+a^2\] から, $f(s)$ は $(a,a^2)$ を頂点とする上に凸の放物線であるので, $t = f(s)$ と $t = b$ が $2$ 個の共有点をもつのは \[ b < a^2\] の場合に限る. ゆえに, $C$ に $2$ 本の接線が引ける点の存在範囲は $C$ の下方である.$y = 2s(x-s)+s^2$ つまり $y = 2sx-s^2$ - (2)
- ①
- $C$ の点 $\mathrm T_k(x_k,y_k)$ $(k = 1,\ 2)$ における接線の方程式は,
\[ y = 2x_kx-y_k\]
である.
これが点 $\mathrm P(a,b)$ を通るとき,
が成り立つ. これは直線 $y+b = 2ax$ が点 $\mathrm T_1,$ $\mathrm T_2$ を通ることを意味しているから, 直線 $\mathrm T_1\mathrm T_2$ の方程式は \[ y+b = 2ax\] である.
$b = 2x_ka-y_k$ つまり $y_k+b = 2ax_k$ - ②
- ① により, 直線 $\mathrm T'_1\mathrm T'_2$ の方程式は $y+b' = 2a'x$ である. 直線 $\mathrm T_1\mathrm T_2$ つまり $y+b = 2ax$ は点 $\mathrm P'(a',b')$ を通るから, \[ b+b' = 2a'a\] が成り立つ. これは, 直線 $\mathrm T'_1\mathrm T'_2$ が点 $\mathrm P(a,b)$ を通ることを意味している.
- ③
- ① により, 直線 $\mathrm T_1\mathrm T_2,$ $\mathrm T'_1\mathrm T'_2,$ $\mathrm T''_1\mathrm T''_2$ の方程式はそれぞれ \[ y+b = 2ax, \quad y+b' = 2a'x, \quad y+b'' = 2a''x\] である. 直線 $\mathrm T_1\mathrm T_2,$ $\mathrm T'_1\mathrm T'_2$ が点 $\mathrm P''(a'',b'')$ を通ることから, \[ b+b'' = 2a''a, \quad b'+b'' = 2a''a'\] が成り立つ. これは, 直線 $\mathrm T''_1\mathrm T''_2$ が点 $\mathrm P(a,b),$ $\mathrm P'(a',b')$ を通ること, つまり直線 $\mathrm T''_1\mathrm T''_2$ が直線 $\mathrm{PP}'$ と一致することを意味している.
参考
- 平行移動, 回転移動, 対称移動と $y$ 座標の定数倍を考えることにより, 次のことがわかる: 放物線 $C$ に $2$ 本の接線が引ける点の存在範囲は, $C$ によって二分された領域のうち, 準線を含む方の領域である.
- 直線 $\mathrm T_1\mathrm T_2$ を点 $\mathrm P$ に関する放物線 $C$ の「極線」(polar line, polar) と呼び, 点 $\mathrm P$ をその「極」(pole) と呼ぶ.
- 点 $\mathrm P$ に関する放物線 $C$ の「極線」を $\mathrm P^*$ で表すとき, (2) ② は
\[\mathrm Q \in \mathrm P^* \iff \mathrm P \in \mathrm Q^*\]
が成り立つということである.
これは, しばしば「共役定理」と呼ばれる.
このことを使うと, 例えば, 点 $\mathrm P_1,$ $\mathrm P_2,$ $\mathrm P_3$ に対して,
$\mathrm Q \in \mathrm P_k{}^*$ $\iff$ $\mathrm P_k \in \mathrm Q^*$ $(k = 1,\ 2,\ 3)$ から,
$\mathrm P_1{}^*,$ $\mathrm P_2{}^*,$ $\mathrm P_3{}^*$ は $1$ 点で交わるの成り立つことがわかる.
$\iff$ $\mathrm P_1,$ $\mathrm P_2,$ $\mathrm P_3$ は $1$ 直線上にある - (2) ②, ③ の結果とこれらの事実は, $2$ 次曲線に一般化される (こちらを参照).
問題《放物線の共通接線と相似》
$a,$ $b$ を $0$ でない相異なる実数とする.
$2$ つの放物線
\[ y = ax^2 \quad \cdots [1], \qquad y = b(x-p)^2+q \quad \cdots [2]\]
が $2$ 本の共通接線 $\ell _1,$ $\ell _2$ をもつとき,
- (1)
- $\ell _1,$ $\ell _2$ の交点 $\mathrm R$ の座標を求めよ.
- (2)
- $[1],$ $[2]$ の頂点をそれぞれ $\mathrm A,$ $\mathrm B$ とおく. $\mathrm{AR}:\mathrm{RB} = |b|:|a|$ であることを示せ.
- (3)
- $[1],$ $[2]$ は点 $\mathrm R$ を中心として $|b|:|a|$ の比で相似であることを示せ.
解答例
- (1)
- 放物線 $[1]$ 上の点 $(t,at^2)$ における接線の方程式は, \[\begin{aligned} y-at^2 &= 2at(x-t) \\ y &= 2atx-at^2 \quad \cdots [3] \end{aligned}\] である. 直線 $[3]$ が放物線 $[2]$ に接するためには, $[2],$ $[3]$ から $y$ を消去して得られる $2$ 次方程式 \[ b(x-p)^2+q = 2atx-at^2\] つまり \[ bx^2-2(bp+at)x+(bp^2+q+at^2) = 0 \quad \cdots [4]\] が重解をもつこと, つまり $[4]$ の判別式 $D$ について \[\frac{D}{4} = (bp+at)^2-b(bp^2+q+at^2) = 0\] つまり \[ a(a-b)t^2+2abpt-bq = 0 \quad \cdots [5]\] となることが必要十分である. 条件から, 放物線 $[1],$ $[2]$ は $2$ 本の共通接線 $l_1,$ $l_2$ をもつので, $a \neq 0,$ $a \neq b$ に注意すると, $[5]$ は $2$ つの実数解 $t_1,$ $t_2$ をもつ. $[5]$ の解と係数の関係により, \[\begin{aligned} t_1+t_2 &= -\frac{2abp}{a(a-b)} = -\frac{2bp}{a-b} \quad \cdots [6], \\ t_1t_2 &= -\frac{bq}{a(a-b)} \quad \cdots [7] \end{aligned}\] が得られる. $l_1,$ $l_2$ は \[ y = 2at_kx-at_k{}^2 \quad (k = 1,\ 2)\] と表せる. $l_1,$ $l_2$ の交点 $\mathrm R$ の $x$ 座標は, \[ 2at_1x-at_1{}^2 = 2at_2x-at_2{}^2\] つまり \[ 2a(t_1-t_2)x = a(t_1+t_2)(t_1-t_2)\] の解であるから, $t_1 \neq t_2$ に注意すると \[ x = \frac{t_1+t_2}{2} = -\frac{bp}{a-b} \quad (\because [6])\] が得られる. $\mathrm R$ の $y$ 座標は, \[ y = 2at_1\cdot\frac{t_1+t_2}{2}-at_1{}^2 = at_1t_2 = -\frac{bq}{a-b} \quad (\because [7])\] である. よって, \[\mathrm R\left( -\frac{bp}{a-b},\ -\frac{bq}{a-b}\right) \quad \cdots [8]\] である.
- (2)
- 放物線 $[1],$ $[2]$ の頂点はそれぞれ \[\mathrm A(0,0) \quad \cdots [9], \qquad \mathrm B(p,q) \quad \cdots [10]\] であるので, $[8]$ から \[\begin{aligned} \mathrm{AR}^2 &= \left( -\frac{bp}{a-b}\right) ^2+\left( -\frac{bq}{a-b}\right) ^2 = \frac{b^2(p^2+q^2)}{(a-b)^2}, \\ \mathrm{BR}^2 &= \left( p+\frac{bp}{a-b}\right) ^2+\left( q+\frac{bq}{a-b}\right) ^2 \\ &= \left(\frac{ap}{a-b}\right) ^2+\left(\frac{aq}{a-b}\right) ^2 = \frac{a^2(p^2+q^2)}{(a-b)^2} \end{aligned}\] である. $[1],$ $[2]$ は $2$ 本の共通接線をもつから $\mathrm A \neq \mathrm B$ であり, したがって \[\mathrm{AR}:\mathrm{BR} = \frac{|b|\sqrt{p^2+q^2}}{|a-b|}:\frac{|a|\sqrt{p^2+q^2}}{|a-b|} = |b|:|a|\] である ($\mathrm{AB} = \sqrt{p^2+q^2} \neq 0$ に注意).
- (3)
- 放物線 $[1]$ 上の点 $\mathrm P(x,y),$ 任意の点 $\mathrm Q(X,Y)$ が点 $\mathrm R$ を中心として $|b|:|a|$ の比で相似であるとする.
$[8]$~$[10]$ から,
$a,$ $b$ が同符号のとき $\mathrm R$ は $\mathrm{AB}$ を $b:a$ の比に外分した点であり,
$a,$ $b$ が異符号のとき $\mathrm R$ は $\mathrm{AB}$ を $-b:a$ の比に内分した点である.
$\mathrm P \neq \mathrm A,$ $\mathrm Q \neq \mathrm B$ のときも, $\triangle\mathrm{APR},$ $\triangle\mathrm{BQR}$ は相似であるから,
$a,$ $b$ が同符号のとき $\mathrm R$ は $\mathrm{PQ}$ を $b:a$ の比に外分した点であり,
$a,$ $b$ が異符号のとき $\mathrm R$ は $\mathrm{PQ}$ を $-b:a$ の比に内分した点である.
よって,
\[\mathrm R\left(\frac{ax-bX}{a-b},\frac{ay-bY}{a-b}\right) \quad \cdots [11]\]
である.
$[8],$ $[11]$ の各座標を比較すると,
\[ x = \frac{b}{a}(X-p), \quad y = \frac{b}{a}(Y-q)\]
となる.
これを $[1]$ に代入すると,
\[\frac{b}{a}(Y-q) = a\left\{\frac{b}{a}(X-p)\right\} ^2 = \frac{b^2}{a}(X-p)^2\]
から
\[ Y = b(X-p)^2+q\]
が得られる.
これは点 $\mathrm Q$ が放物線 $[2]$ 上にあることを意味する.
同様に, 放物線 $[2]$ 上の点 $\mathrm Q,$ 任意の点 $\mathrm P$ が点 $\mathrm R$ を中心として $|b|:|a|$ の比で相似であるとき, 点 $\mathrm P$ は放物線 $[1]$ 上にある.
ゆえに, 放物線 $[1],$ $[2]$ は点 $\mathrm R$ を中心として $|b|:|a|$ の比で相似である.
参考
$a_1,$ $a_2$ を $0$ でない相異なる実数とする.
$2$ つの $2$ 次関数のグラフ
\[\begin{aligned}
C_1:y &= a_1(x-p_1)^2+q_1, \\
C_2:y &= a_2(x-p_2)^2+q_2
\end{aligned}\]
は $x$ 軸方向に $-p_1,$ $y$ 軸方向に $-q_1$ だけ平行移動すると
\[\begin{aligned}
y &= a_1x^2, \\
y &= a_2(x-p)^2+q \quad (p = p_2-p_1,\ q = q_2-q_1)
\end{aligned}\]
に移され, 平行移動によって $2$ つの図形の相似関係は保たれるから,
$C_1,$ $C_2$ が $2$ 本の共通接線をもつとき,
$C_1,$ $C_2$ は共通接線の交点 $\left(\dfrac{a_1p_1-a_2p_2}{a_1-a_2},\dfrac{a_1q_1-a_2q_2}{a_1-a_2}\right)$ を中心として $|a_2|:|a_1|$ の比で相似である.
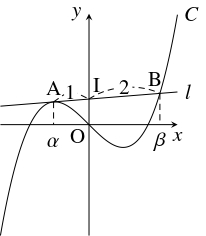
問題《$3$ 次関数のグラフの接線の分割比》
$3$ 次関数 $f(x) = x^3+px$ ($p$: 実数) のグラフ $C:y = f(x)$ の点 $\mathrm A(\alpha,f(\alpha ))$ における接線 $l:y = g(x)$ と $C$ の交点を $\mathrm B(\beta,f(\beta ))$ $(\beta \neq \alpha )$ とおき,
$l$ の $y$ 切片を $\mathrm I$ とおく.
\[\mathrm{AI}:\mathrm{IB} = 1:2\]
であることを示せ.
多項式関数のグラフ $y = f(x)$ とその点 $(\alpha,f(\alpha ))$ における接線 $y = g(x)$ について $f(x)-g(x)$ が $(x-\alpha )^2$ で割り切れること (こちらを参照)は証明なしに使ってよい.
解答例
$f(\beta )-g(\beta ) = 0$ であるから, 因数定理により $f(x)-g(x)$ は $x-\beta$ で割り切れる.
よって,
\[ f(x)-g(x) = (x-\alpha )^2(x-\beta )\]
が成り立つ.
$f(x)$ の形と $g(x)$ が $1$ 次関数であることから $f(x)-g(x)$ の $x^2$ の項の係数は $0$ であり,
右辺の $x^2$ の項の係数は $-(2\alpha +\beta )$ であるから,
が成り立つ.
よって,
\[\mathrm{AI}:\mathrm{IB} = |\alpha |:|\beta | = |\alpha |:|-2\alpha | = 1:2\]
が成り立つ.
| $0 = -(2\alpha +\beta )$ つまり $\beta = -2\alpha$ |

参考
一般に, $3$ 次関数のグラフ $C:y = f(x)$ の接線において, 接点 $\mathrm A$ ともう $1$ つの共有点 $\mathrm B$ を結ぶ線分は, $C$ の対称の中心を通り $y$ 軸に平行な直線によって $1:2$ の比に内分される.
この定理の証明は, 平行移動と $y$ 軸方向の拡大・縮小により, 本問の場合に帰着される.