ペル方程式
ペル方程式
定義《ペル方程式》
$d$ を平方数でない正の整数とする.
$x^2-dy^2 = 1$ または $x^2-dy^2 = -1$ の形の方程式を ペル方程式(Pell's equation)と呼ぶ.
$(\pm 1,0)$ を $x^2-dy^2 = 1$ の自明解(trivial solution)と呼ぶ.
注意
$d$ が平方数のとき, 整数の範囲で
\[ x^2-dy^2 = (x+y\sqrt d)(x-y\sqrt d)\]
と因数分解でき, 積が $\pm 1$ であるような整数は $1$ と $-1$ に限るから,
$x^2-dy^2 = 1$ の解は $(x,y) = (\pm 1,0)$ に限り, $x^2-dy^2 = -1$ の解が存在するのは $d = 1$ の場合に限ることが分かる.
これは $d$ が平方数でないときの解の様子とまったく異なるので, $d$ が平方数の場合は除外して考える.
定理《$x^2-dy^2 = 1$ の解の存在》
$d$ を平方数でない正の整数とする.
このとき, $x^2-dy^2 = 1$ は無限個の整数解を持つ.
ペル方程式の解の構造
定理《ペル方程式の解の構造》
$d$ を平方数でない正の整数とする.
- (a)
- $x^2-dy^2 = 1$ の正の整数解について, $x+y\sqrt d$ の最小値を $\varepsilon$ とおく. このとき, 各正の整数 $n$ に対して \[\varepsilon ^n = x_n+y_n\sqrt d\] で定まる $(x,y) = (x_n,y_n)$ が $x^2-dy^2 = 1$ のすべての正の整数解を与える.
- (b)
- $x^2-dy^2 = -1$ の整数解が存在するとして, その正の整数解について $x+y\sqrt d$ の最小値を $\varepsilon$ とおく. このとき, 各正の整数 $n$ に対して \[\varepsilon ^{2n-1} = x_n+y_n\sqrt d\] で定まる $(x,y) = (x_n,y_n)$ が $x^2-dy^2 = -1$ のすべての正の整数解を与える.
補題《共役の乗法性》
$d$ を平方数でない正の整数とする.
$a,$ $b$ が整数のとき,
\[\widetilde{a+b\sqrt d} = a-b\sqrt d\]
と定める.
$a_1,$ $b_1,$ $a_2,$ $b_2$ が整数のとき, $\alpha _k = a_k+b_k\sqrt d\ (k = 1,2)$ について, $\widetilde{\alpha _1\alpha _2} = \widetilde{\alpha _1}\cdot\widetilde{\alpha _2}$ が成り立つ.
補題の証明
$\alpha _1\alpha _2 = (a_1a_2+b_1b_2d)+(a_1b_2+b_1a_2)\sqrt d$ から,
\[\begin{aligned}
&\widetilde{\alpha _1}\cdot\widetilde{\alpha _2} = (a_1-b_1\sqrt d)(a_2-b_2\sqrt d) \\
&= (a_1a_2+b_1b_2d)-(a_1b_2+b_1a_2)\sqrt d = \widetilde{\alpha _1\alpha _2}
\end{aligned}\]
が成り立つ.
定理の証明
- (a)
- 補題と $\varepsilon\tilde\varepsilon = 1$ から, \[\begin{aligned} x_n{}^2-dy_n{}^2 &= (x_n+y_n\sqrt d)(x_n-y_n\sqrt d) \\ &= \varepsilon ^n\widetilde{\varepsilon ^n} = \varepsilon ^n\tilde\varepsilon ^n = (\varepsilon\tilde\varepsilon )^n \\ &= 1^n = 1 \end{aligned}\] が成り立つ. さらに, $(x,y)$ を $x^2-dy^2 = 1$ の正の整数解とする. このとき, $\varepsilon > 1$ から, \[\varepsilon ^n \leqq x+y\sqrt d < \varepsilon ^{n+1}\] を満たす正の整数 $n$ が存在する. 両辺を $\varepsilon ^n$ で割ると, \[ 1 \leqq (x+y\sqrt d)\varepsilon ^{-n} < \varepsilon\] となる. \[\begin{aligned} &(x+y\sqrt d)\varepsilon ^{-n} = (x+y\sqrt d)\tilde\varepsilon ^n \\ &= (x+y\sqrt d)\widetilde{\varepsilon ^n} = (x+y\sqrt d)(x_n-y_n\sqrt d) \\ &= x'+y'\sqrt d \end{aligned}\] を満たす整数 $x',$ $y'$ をとる. 補題により \[ (x-y\sqrt d)\tilde\varepsilon ^{-n} = x'-y'\sqrt d\] が成り立つので, 辺々を掛けあわせると \[ x'^2-dy'^2 = (x^2-dy^2)(\varepsilon\tilde\varepsilon )^{-n} = 1\cdot 1^{-n} = 1\] が得られる. よって, $\varepsilon$ の最小性により, $x'+y'\sqrt d = 1$ が成り立つ. これから $x+y\sqrt d = \varepsilon ^n$ が得られる.
- (b)
- 補題と $\varepsilon\tilde\varepsilon = -1$ から, \[\begin{aligned} x_n{}^2-dy_n{}^2 &= (x_n+y_n\sqrt d)(x_n-y_n\sqrt d) \\ &= \varepsilon ^{2n-1}\widetilde{\varepsilon ^{2n-1}} = \varepsilon ^{2n-1}\tilde\varepsilon ^{2n-1} = (\varepsilon\tilde\varepsilon )^{2n-1} \\ &= (-1)^{2n-1} = -1 \end{aligned}\] が成り立つ. さらに, $(x,y)$ を $x^2-dy^2 = -1$ の正の整数解とする. このとき, $\varepsilon > 1$ から, \[\varepsilon ^{2n-1} \leqq x+y\sqrt d < \varepsilon ^{2n+1}\] を満たす正の整数 $n$ が存在する. 両辺を $\varepsilon ^{2n-1}$ で割ると, \[ 1 \leqq (x+y\sqrt d)\varepsilon ^{1-2n} < \varepsilon ^2\] となる. \[\begin{aligned} &(x+y\sqrt d)\varepsilon ^{1-2n} = (x+y\sqrt d)\tilde\varepsilon ^{2n-1} \\ &= (x+y\sqrt d)\widetilde{\varepsilon ^{2n-1}} = (x+y\sqrt d)(x_n-y_n\sqrt d) \\ &= x'+y'\sqrt d \end{aligned}\] を満たす整数 $x',$ $y'$ をとる. 補題により \[ (x-y\sqrt d)\tilde\varepsilon ^{1-2n} = x'-y'\sqrt d\] が成り立つので, 辺々を掛けあわせると \[\begin{aligned} x'^2-dy'^2 &= (x^2-dy^2)(\varepsilon\tilde\varepsilon )^{1-2n} \\ &= (-1)\cdot (-1)^{1-2n} = 1 \end{aligned}\] が得られる. $x^2-dy^2 = 1$ の正の整解について $x+y\sqrt d$ の最小値は $\varepsilon ^2$ であるから, $x'+y'\sqrt d = 1$ が成り立つ. これから $x+y\sqrt d = \varepsilon ^{2n-1}$ が得られる.
定理《ペル方程式の平方根の近似計算への応用》
$d$ を平方数でない正の整数とする.
$x^2-dy^2 = 1$ の正の整数解について, $x+y\sqrt d$ の値が小さい順に $(x_n,y_n)$ とおくと, $x_n/y_n$ は $\sqrt d$ に収束する.
問題
数学 A: 整数の性質
問題《ペル方程式の一般解》
- (1)
- $\alpha = x+y\sqrt 2$ ($x,$ $y$: 整数)の形に表される各実数 $\alpha$ に対して, $\widetilde{\alpha} = x-y\sqrt 2$ と定める. $\alpha = x+y\sqrt 2,$ $\alpha ' = x'+y'\sqrt 2$ ($x,$ $y,$ $x',$ $y'$: 整数)のとき, $\widetilde{\alpha\alpha '} = \widetilde{\alpha}\widetilde{\alpha '}$ が成り立つことを示せ.
- (2)
- $x^2-2y^2 = 1$ の正の整数解 $(x,y)$ を用いて $x+y\sqrt 2$ の形に表される実数の最小値を $\varepsilon$ とおく. $\varepsilon$ の値を求めよ.
- (3)
- $n$ を正の整数とするとき, \[\varepsilon ^n = x_n+y_n\sqrt 2 \quad \cdots [\mathrm A]\] により定まる整数 $x_n,$ $y_n$ について, $(x,y) = (x_n,y_n)$ は $x^2-2y^2 = 1$ の解であることを示せ. さらに, $\varepsilon,$ $\widetilde{\varepsilon}$ と $n$ を用いて $x_n,$ $y_n$ を表せ.
- (4)
- $(x,y)$ を $x^2-2y^2 = 1$ の正の整数解とする. このとき, $(x,y)$ はある正の整数 $n$ に対して上記の解 $(x_n,y_n)$ に一致することを示せ.
解答例
こちらを参照.
問題《解をもたないペル方程式》
方程式 $x^2-3y^2 = -1$ は整数解をもたないことを示せ.
解答例
こちらを参照.
数学 II: 式と証明
問題《ブラーマグプタの恒等式とペル方程式》
- (1)
- $(xu+dyv)^2-d(xv+yu)^2 = (x^2-dy^2)(u^2-dv^2)$ が成り立つことを示せ.
- (2)
- $u^2-2v^2 = 1$ の正の整数解を $1$ つ求めよ.
- (3)
- $x^2-2y^2 = -1$ は無限に多くの整数解を持つことを示せ.
解答例
こちらを参照.
数学 B: 数列
問題《平方三角数とペル方程式》
- (1)
- 図のように, $l$ 行 $l$ 列の正方形の形に並べられていた石を崩した後, $1$ 段目に $1$ 個, $\cdots,$ $k$ 段目に $k$ 個, $\cdots$ と $m$ 段目まで並べていくと, 石を余すことなく正三角形の形に並べられたとする.
このとき, $(x,y) = (2m+1,2l)$ は $x^2-2y^2 = 1$ の解であることを示せ.
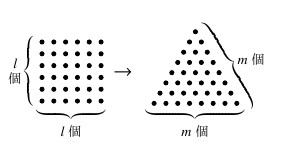
- (2)
- $(x,y)$ を $x^2-2y^2 = 1$ の正の整数解とする.
このとき, $x$ は $3$ 以上の奇数であり, $y$ は偶数であることを示せ.
さらに, $l = \dfrac{y}{2},$ $m = \dfrac{x-1}{2}$ とおくと, 上記のように, $l$ 行 $l$ 列の正方形の形に並べられた石は, $m$ 段の正三角形の形にも並べられることを示せ.
(参考: 津田塾大)
解答例
こちらを参照.
問題《ペル方程式に関する連立漸化式》
数列 $\{ x_n\},$ $\{ y_n\}$ を
\[ x_1 = 3,\ y_1 = 2,\ x_{n+1} = 3x_n+4y_n,\ y_{n+1} = 2x_n+3y_n\]
で定める.
- (a)
- 数列 $\{ x_n+ky_n\}$ が公比 $r$ の等比数列となるような定数 $k,$ $r$ の組を $2$ 組求めよ. さらに, 数列 $\{ x_n\},$ $\{ y_n\}$ の一般項を求めよ.
- (b)
- $x_n,$ $x_{n+1},$ $x_{n+2}$ の関係式を求めよ. また, 数列 $\{ x_{n+1}-\alpha x_n\}$ が公比 $\beta$ の等比数列となるような定数 $\alpha,$ $\beta$ の組を $2$ 組求めよ. さらに, 数列 $\{ x_n\},$ $\{ y_n\}$ の一般項を求めよ.
解答例
こちらを参照.