空間図形
多面体
問題《正多面体の種類》
- (1)
- 各面が正 $p$ 角形であり, 各頂点に $q$ 本の辺が集まるような正多面体 (凸多面体) について, $(p-2)(q-2) < 4$ が成り立つことを示せ.
- (2)
- 正多面体 (凸多面体) は, 正四面体, 正六面体, 正八面体, 正十二面体, 正二十面体の $5$ つに限ることを示せ.
解答例
- (1)
- 各面が正 $p$ 角形であり, 各頂点に $q$ 本の辺が集まるような正多面体 (凸多面体) において, 各頂点に集まる角の大きさの和は $360^\circ$ 未満である. 正 $p$ 角形の内角の大きさは $(p-2)\times 180^\circ\div p$ であるから, \[\frac{180(p-2)}{p}\cdot q < 360\] が成り立つ. 整理すると, \[\begin{aligned} (p-2)q &< 2p \\ pq-2p-2q &< 0 \\ (p-2)(q-2) &< 4 \quad \cdots [1] \end{aligned}\] となる.
- (2)
- $p \geqq 3,$ $q \geqq 3$ に注意すると, $[1]$ から \[\begin{aligned} (p-2,q-2) &= (1,1),\ (2,1),\ (1,2),\ (3,1),\ (1,3) \\ (p,q) &= (3,3),\ (4,3),\ (3,4),\ (5,3),\ (3,5) \end{aligned}\] が得られる. この条件を満たす正多面体として, それぞれ正四面体, 正六面体, 正八面体, 正十二面体, 正二十面体がある.
別解
- (1)
- 頂点の数を $v,$ 辺の数を $e,$ 面の数を $f$ とおく. このとき, オイラーの多面体定理により, \[ v-e+f = 2\] が成り立つ. $1$ 本の辺は $2$ 頂点を結び, $2$ 面に接するから, \[ qv = pf = 2e\] である. これらの式から, \[\begin{aligned} \frac{2e}{q}-e+\frac{2e}{p} &= 2 \\ \frac{1}{p}+\frac{1}{q}-\frac{1}{2} &= \frac{1}{e} \end{aligned}\] が得られる. 右辺は正であるから, 左辺も正であり, \[\begin{aligned} \frac{1}{p}+\frac{1}{q} &> \frac{1}{2} \\ 2q+2p &> pq \\ pq-2p-2q &< 0 \\ (p-2)(q-2) &< 4 \end{aligned}\] が成り立つ.
参考
正多面体 (凸多面体) が正四面体, 正六面体, 正八面体, 正十二面体, 正二十面体の $5$ つに限ることは, テアイテトスによって証明された.
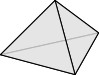
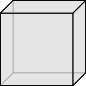
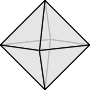
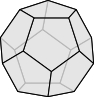





※$2022/05/13$『不等式の整数解』から移動
問題《垂線の足の位置による正四面体の特徴付け》
次は同値であることを示せ.
- (i)
- 四面体 $\mathrm{ABCD}$ は正四面体である.
- (ii)
- 四面体 $\mathrm{ABCD}$ の各頂点から対面に下ろした垂線の足はその面の外心である.
(参考: $2016$ 京都大)
解答例
- (i) $\Longrightarrow$ (ii) を示すため, (i) を仮定する. 頂点 $\mathrm D$ から面 $\mathrm{ABC}$ に下ろした垂線の足を $\mathrm H$ とおく. このとき, 直角三角形 $\mathrm{ADH},$ $\mathrm{BDH},$ $\mathrm{CDH}$ は, 斜辺 $\mathrm{AD},$ $\mathrm{BD},$ $\mathrm{CD}$ の長さが等しく, $\mathrm{DH}$ を共通の辺にもつから, 合同である. よって, $\mathrm{AH} = \mathrm{BH} = \mathrm{CH}$ であるから, $\mathrm H$ は $\triangle\mathrm{ABC}$ の外心である. 同様に, 他の頂点から対面に下ろした垂線の足もその面の外心である.
- (ii) $\Longrightarrow$ (i) を示すため, (ii) を仮定する. 頂点 $\mathrm D$ から面 $\mathrm{ABC}$ に下ろした垂線の足を $\mathrm H$ とおく. このとき, 三角形 $\mathrm{ADH},$ $\mathrm{BDH},$ $\mathrm{CDH}$ は, 辺 $\mathrm{AH},$ $\mathrm{BH},$ $\mathrm{CH}$ の長さが等しく, $\mathrm{DH}$ を共通の辺にもち, $\angle\mathrm{AHD} = \angle\mathrm{BHD} = \angle\mathrm{CHD} = 90^\circ$ であるから, 合同である. よって, $\mathrm{AD} = \mathrm{BD} = \mathrm{CD}$ である. 同様に, 残りの辺の長さもこれらの辺の長さに等しいから, 四面体 $\mathrm{ABCD}$ は正四面体である.
