凸関数
凸関数
定義《凸関数》
$f(x)$ を区間 $I$ で定義された実数値関数とする.
- $f(x)$ のグラフがその上の $2$ 点を結ぶ線分よりも下方にあるとき, つまり $(a,b) \subset I,$ $0 < t < 1$ ならば
\[ f((1-t)a+tb) \leqq (1-t)f(a)+tf(b)\]
が成り立つとき, $f(x)$ は下に凸 (convex downward) であるという.
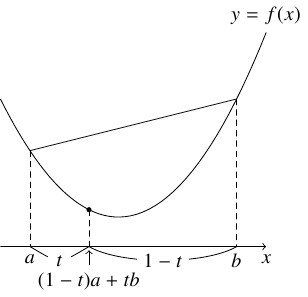
- $f(x)$ のグラフがその上の $2$ 点を結ぶ線分よりも上方にあるとき, つまり $(a,b) \subset I,$ $0 < t < 1$ ならば \[ f((1-t)a+tb) \geqq (1-t)f(a)+tf(b)\] が成り立つとき, $f(x)$ は上に凸 (convex upward) であるという.
定理《凸関数の特徴付け》
区間 $I$ で定義された実数値関数 $f(x)$ について, 次は同値である.
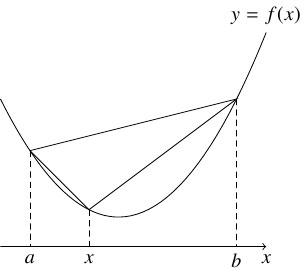
- (i)
- $f(x)$ は下に凸である.
- (ii)
- $(a,b) \subset I,$ $a < x < b$ ならば \[\frac{f(x)-f(a)}{x-a} \leqq \frac{f(b)-f(x)}{b-x}\] が成り立つ.
- (ii)'
- $(a,b) \subset I,$ $a < x < b$ ならば \[\frac{f(x)-f(a)}{x-a} \leqq \frac{f(b)-f(a)}{b-a} \leqq \frac{f(b)-f(x)}{b-x}\] が成り立つ.

証明
$(a,b) \subset I,$ $a < x < b,$ $x = (1-t)a+tb,$ $0 < t < 1$ のとき,
\[\begin{aligned}
&(b-x)(f(x)-f(a))-(x-a)(f(b)-f(x)) \\
&= (b-a)f(x)-(b-x)f(a)-(x-a)f(b) \quad \cdots [1] \\
&= (b-a)f(x)-(1-t)(b-a)f(a)-t(b-a)f(b) \\
&= (b-a)(f(x)-(1-t)f(a)-tf(b))
\end{aligned}\]
が成り立つから (i) と (ii) は同値であり,
\[ (b-a)(f(x)-f(a))-(x-a)(f(b)-f(a))\]
と
\[ (b-x)(f(b)-f(a))-(b-a)(f(b)-f(x))\]
はいずれも $[1]$ に等しいから (ii) と (ii)' も同値である.
Jensen の不等式
定理《Jensen の不等式》
区間 $I$ で定義された実数値関数 $f(x)$ について, 次は同値である.
- (i)
- $f(x)$ は下に凸である.
- (i)'
- $2$ 以上のすべての整数 $n$ に対して, $x_1,\ \cdots,\ x_n \in I,$ $t_1,\ \cdots,\ t_n \in (0,1),$ $\sum_{k = 1}^nt_k = 1$ ならば \[ f\left(\sum_{k = 1}^nt_kx_k\right) \leqq \sum_{k = 1}^nt_kf(x_k)\] が成り立つ.
証明
(i) $\Longrightarrow$ (i)' の証明: (i) が成り立つとする.
このとき, (i)' の $n = 2$ の場合が成り立つ.
与えられた $2$ 以上の整数 $n$ に対して, (i)' の主張が成り立つとする.
$x_1,\ \cdots,\ x_n,\ x_{n+1} \in I,$ $t_1,\ \cdots,\ t_n,\ t_{n+1} \in (0,1),$ $\sum_{k = 1}^{n+1}t_k = 1$ のとき,
$s = \sum_{k = 1}^nt_k$ とおくと $s+t_{n+1} = 1$ となるから,
\[\begin{aligned}
f\left(\sum_{k = 1}^{n+1}t_kx_k\right) &= f\left( s\sum_{k = 1}^n\frac{t_k}{s}x_k+t_{n+1}x_{n+1}\right) \\
&\leqq sf\left(\sum_{k = 1}^n\frac{t_k}{s}x_k\right)+t_{n+1}f(x_{n+1}) \\
&\leqq s\sum_{k = 1}^n\frac{t_k}{s}f(x_k)+t_{n+1}f(x_{n+1}) \\
&= \sum_{k = 1}^{n+1}t_kf(x_k)
\end{aligned}\]
となる.
以上から, すべての正の整数 $n$ に対して (i)' の主張が成り立つ.
(i)' $\Longrightarrow$ (i) の証明: (i) は (i)' の $n = 2$ の場合に他ならない.
(i)' $\Longrightarrow$ (i) の証明: (i) は (i)' の $n = 2$ の場合に他ならない.
注意
(i)' の不等式は Jensen の不等式と呼ばれ,
$n \geqq 3$ であり, $x_1,$ $\cdots,$ $x_n$ が相異なるとき, $f(x)$ のグラフ $y = f(x)$ 上の $n$ 個の点 $(x_1,f(x_1)),$ $\cdots,$ $(x_n,f(x_n))$ を結ぶ $n$ 角形の内部の点が $y = f(x)$ よりも上側にあることを意味する.
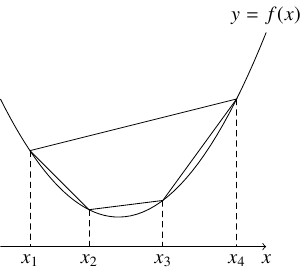

例《Young の不等式》
$p > 1,$ $q > 1,$ $\dfrac{1}{p}+\dfrac{1}{q} = 1$ として, $f(x) = e^x,$ $t_1 = \dfrac{1}{p},$ $t_2 = \dfrac{1}{q}$ にイェンセンの不等式を適用すると,
\[\frac{e^x}{p}+\frac{e^y}{q} \geqq e^{\frac{x}{p}+\frac{y}{q}} = e^{\frac{x}{p}}e^{\frac{y}{q}}\]
が得られる.
$a > 0,$ $b > 0$ として, $x = p\log a,$ $y = q\log b$ を代入すると, ヤングの不等式
\[\frac{a^p}{p}+\frac{b^q}{q} \geqq ab\]
が得られる.
凸関数のグラフの接線
定理《凸関数のグラフの接線による特徴付け》
区間 $I$ で定義された微分可能な実数値関数 $f(x)$ について, 次は同値である.
- (i)
- $f(x)$ は下に凸である.
- (iii)
- $\alpha \in I$ ならば \[ f'(\alpha )(x-\alpha )+f(\alpha ) \leqq f(x)\] が成り立つ.
証明
(i) $\Longrightarrow$ (iii) の証明: (i) が成り立つとする.
$\alpha,$ $x \in I,$ $x \neq \alpha,$ $0 < t < 1$ のとき, (i) から
\[ f((1-t)\alpha +tx) \leqq (1-t)f(\alpha )+tf(x),\]
よって
\[\begin{aligned}
&(1-t)\frac{f(\alpha +t(x-\alpha ))-f(\alpha )}{t(x-\alpha )}(x-\alpha ) \\
&\qquad\qquad\qquad\leqq f(x)-f(\alpha +t(x-\alpha ))
\end{aligned}\]
が成り立つので, $t \to 0$ とすると $f(x)$ の微分可能性とそれが導く連続性から
\[ f'(\alpha )(x-\alpha ) \leqq f(x)-f(\alpha )\]
が得られる.
また, $x = \alpha \in I$ のとき, この不等式の等号が成り立つ.
よって, (iii) が成り立つ.
(i) $\Longrightarrow$ (iii) の証明: (iii) が成り立つとする. $(a,b) \subset I,$ $0 < t < 1$ とし, $\alpha = (1-t)a+tb$ とおくと, (iii) から \[\begin{aligned} f'(\alpha )(a-\alpha )+f(\alpha ) &\leqq f(a) \quad \cdots [2], \\ f'(\alpha )(b-\alpha )+f(\alpha ) &\leqq f(b) \quad \cdots [3] \end{aligned}\] が成り立つので, $(1-t)\times [2]+t\times [3]$ から \[ f((1-t)a+tb) = f(\alpha ) \leqq (1-t)f(a)+tf(b)\] が得られる. よって, (i) が成り立つ.
(i) $\Longrightarrow$ (iii) の証明: (iii) が成り立つとする. $(a,b) \subset I,$ $0 < t < 1$ とし, $\alpha = (1-t)a+tb$ とおくと, (iii) から \[\begin{aligned} f'(\alpha )(a-\alpha )+f(\alpha ) &\leqq f(a) \quad \cdots [2], \\ f'(\alpha )(b-\alpha )+f(\alpha ) &\leqq f(b) \quad \cdots [3] \end{aligned}\] が成り立つので, $(1-t)\times [2]+t\times [3]$ から \[ f((1-t)a+tb) = f(\alpha ) \leqq (1-t)f(a)+tf(b)\] が得られる. よって, (i) が成り立つ.
凸関数の第 $2$ 次導関数
定理《凸関数の第 $2$ 次導関数の符号による特徴付け》
区間 $I$ で定義された $2$ 回微分可能な実数値関数 $f(x)$ について, 次は同値である.
- (i)
- $f(x)$ は下に凸である.
- (iv)
- $f''(x) \geqq 0$ が成り立つ.
- (iv)'
- $f(x)$ のグラフ $y = f(x)$ の点 $(x,f(x))$ における接線の傾きは単調増加である.
証明
$f''(x) \geqq 0$ は $f'(x)$ が単調増加であることを意味し,
$f(x)$ のグラフ $y = f(x)$ の点 $(x,f(x))$ における接線の傾きは $f'(x)$ であるから,
(iv) と (iv)' は同値である.
(i) は (ii), (ii)' と同値であるから, (i) $\iff$ (iv) を示すには, (ii)' $\Longrightarrow$ (iv) と (iv) $\Longrightarrow$ (ii) を示せば良い.
(ii)' $\Longrightarrow$ (iv) の証明: (ii)' が成り立つとすると, $(a,b) \subset I$ のとき, $a < x < b$ において \[\frac{f(x)-f(a)}{x-a} \leqq \frac{f(b)-f(a)}{b-a} \leqq \frac{f(b)-f(x)}{b-x}\] が成り立ち, 左側の不等式で $x \to a+0$ として, 右側の不等式で $x \to b-0$ とすると \[ f'(a) \leqq \frac{f(b)-f(a)}{b-a} \leqq f'(b)\] となるから, (iv) が成り立つ.
(iv) $\Longrightarrow$ (ii) の証明: (iv) が成り立つとすると, $(a,b) \subset I,$ $a < x < b$ のとき, 平均値の定理により存在が保証される \[\begin{aligned} \frac{f(x)-f(a)}{x-a} = f'(c), \quad&\quad \frac{f(b)-f(x)}{b-x} = f'(d), \\ a < c < &x < d < b \end{aligned}\] なる実数 $c,$ $d$ に対して $f'(c) \leqq f'(d)$ となるから, (ii) が成り立つ.
(i) は (ii), (ii)' と同値であるから, (i) $\iff$ (iv) を示すには, (ii)' $\Longrightarrow$ (iv) と (iv) $\Longrightarrow$ (ii) を示せば良い.
(ii)' $\Longrightarrow$ (iv) の証明: (ii)' が成り立つとすると, $(a,b) \subset I$ のとき, $a < x < b$ において \[\frac{f(x)-f(a)}{x-a} \leqq \frac{f(b)-f(a)}{b-a} \leqq \frac{f(b)-f(x)}{b-x}\] が成り立ち, 左側の不等式で $x \to a+0$ として, 右側の不等式で $x \to b-0$ とすると \[ f'(a) \leqq \frac{f(b)-f(a)}{b-a} \leqq f'(b)\] となるから, (iv) が成り立つ.
(iv) $\Longrightarrow$ (ii) の証明: (iv) が成り立つとすると, $(a,b) \subset I,$ $a < x < b$ のとき, 平均値の定理により存在が保証される \[\begin{aligned} \frac{f(x)-f(a)}{x-a} = f'(c), \quad&\quad \frac{f(b)-f(x)}{b-x} = f'(d), \\ a < c < &x < d < b \end{aligned}\] なる実数 $c,$ $d$ に対して $f'(c) \leqq f'(d)$ となるから, (ii) が成り立つ.
高校数学の問題
指数関数・対数関数
問題《対数関数の凸性に関する対数の比較》
$a > 1,$ $P > 0,$ $Q > 0$ のとき,
\[ A = \log_a(P+Q)-\log_a2, \quad G = \dfrac{1}{2}(\log_aP+\log_aQ)\]
の大小を比較せよ.
解答例
こちらを参照.
関数と極限
問題《無理関数を含む不等式とその応用》
$a,$ $b$ を正の数とする.
- (1)
- $a < b$ のとき, 不等式 $\sqrt x > \dfrac{\sqrt b-\sqrt a}{b-a}(x-a)+\sqrt a$ を解け.
- (2)
- $\dfrac{a+b}{2} \geqq \sqrt{ab}$ が成り立つことを示し, 等号成立条件を求めよ.
解答例
こちらを参照.
微分法 (理系)
問題《イェンセンの不等式とその応用》
$n$ を $2$ 以上の整数とする.
- (1)
- $0 < x_1 < x < x_2$ のとき, 平均値の定理を使って \[\frac{\log x-\log x_1}{x-x_1} > \frac{\log x_2-\log x}{x_2-x}\] が成り立つことを示せ. さらに, それを使って \[\log x > \log x_1+\frac{\log x_2-\log x_1}{x_2-x_1}(x-x_1)\] が成り立つことを示せ.
- (2)
- $t_1,$ $\cdots,$ $t_n > 0,$ $t_1+\cdots +t_n = 1$ とする. $x_1,$ $\cdots,$ $x_n > 0$ のとき, \[\log\left(\sum_{k = 1}^nt_kx_k\right) \geqq \sum_{k = 1}^nt_k\log x_k \quad \cdots [*]\] が成り立つことを示せ. また, 等号成立条件を求めよ.
- (3)
- $x_1,$ $\cdots,$ $x_n > 0$ のとき, \[\frac{x_1+\cdots +x_n}{n} \geqq \sqrt[n]{x_1\cdots x_n}\] が成り立つことを示せ. また, 等号成立条件を求めよ.
(参考: $2006$ 滋賀医科大)
解答例
こちらを参照.
問題《凸関数のグラフの接線》
実数値関数 $f(x)$ が点 $x = a$ を含む開区間 $I$ で $2$ 回微分可能であるとし, 曲線 $y = f(x)$ の点 $(a,\ f(a))$ における接線を $y = g(x)$ とする.
このとき, 区間 $I$ において
\[ f''(x) \leqq 0 \Longrightarrow f(x) \leqq g(x)\]
が成り立つことを示せ.
解答例
こちらを参照.
問題《円に内接する $n$ 角形の周長・面積の最大値》
- (1)
- $n$ を $2$ 以上の整数とし, $t_1,$ $\cdots,$ $t_n > 0,$ $t_1+\cdots +t_n = 1$ とする. $x_1,$ $\cdots,$ $x_n \in (0,\pi )$ のとき, \[\sin\left(\sum_{k = 1}^nt_kx_k\right) \geqq \sum_{k = 1}^nt_k\sin x_k\] が成り立つことを示せ. また, 等号成立は $x_1 = \cdots = x_n$ の場合に限ることを示せ.
- (2)
- $3$ 以上の整数 $n$ に対して, 単位円に内接する $n$ 角形のうち周の長さ $L$ が最大になるもの, 面積 $S$ が最大になるものは正 $n$ 角形であることを示せ.
(参考: $2022$ 大阪公立大)
解答例
こちらを参照.